ps: 课题来自于泥卓的课后作业 ps: 建议把页面markdown自己放到vscode或者typora上, 因为本站的markdown似乎没有办法显示Latex语法
实验器材与工具
处理器:13th Gen Intel(R) Core(TM) i7-13700H 2.40 GHz
机带RAM: 16.0GB(15.7GB可用)
WSL 版本: 2.3.24.0
内核版本: 5.15.153.1-2
WSLg 版本: 1.0.65
MSRDC 版本: 1.2.5620
Direct3D 版本: 1.611.1-81528511
DXCore 版本: 10.0.26100.1-240331-1435.ge-release
Windows 版本: 10.0.22631.4317
g++ 版本:11.4.0
nvidia-cuda-toolkit: 12.3
矩阵乘法优化算法
存在矩阵M(m*n)和矩阵N(n*t)做矩阵乘法,按照矩阵乘法的定义,一共需要做m*n*t次乘法计算,以及m*n*t次加法计算,不难理解如果可以减少运算的次数,那么就会产生直观的优化效果
Strassen算法
由上述分析,一般的矩阵运算需要O(n\^3)的复杂度,但Strassen算法通过分治的思想,将大矩阵化成小矩阵, 可以将这个值降至约O(n\^2.81)
如图,将两个4*4矩阵分割为四个分块矩阵,
$
A = \begin{bmatrix}
\begin{pmatrix}a_{11}&a_{12}\a_{21}&a_{22}\end{pmatrix} & \begin{pmatrix}a_{31}&a_{32}\a_{41}&a_{42}\end{pmatrix}
\begin{pmatrix}a_{51}&a_{52}\a_{61}&a_{62}\end{pmatrix} & \begin{pmatrix}a_{71}&a_{72}\a_{81}&a_{82}\end{pmatrix}
\end{bmatrix} = \begin{bmatrix}A_1 & A_2 \ A_3 & A_4\end{bmatrix}
B = \begin{bmatrix}
\begin{pmatrix}b_{11}&b_{12}\b_{21}&b_{22}\end{pmatrix} & \begin{pmatrix}b_{31}&b_{32}\b_{41}&b_{42}\end{pmatrix}
\begin{pmatrix}b_{51}&b_{52}\b_{61}&b_{62}\end{pmatrix} & \begin{pmatrix}b_{71}&b_{72}\b_{81}&b_{82}\end{pmatrix}
\end{bmatrix} = \begin{bmatrix}B_1 & B_2 \ B_3 & B_4\end{bmatrix}
$
此时,$C_{11}$和矩阵$C$的计算方式如下
$
C_{11} = \left(\begin{pmatrix}a_{11}&a_{12}\a_{21}&a_{22}\end{pmatrix}\begin{pmatrix}b_{11}&b_{12}\b_{21}&b_{22}\end{pmatrix}\right)+\left(\begin{pmatrix}a_{31}&a_{32}\a_{41}&a_{42}\end{pmatrix}\begin{pmatrix}b_{51}&b_{52}\b_{61}&b_{62}\end{pmatrix}\right)
$
$
C = \begin{bmatrix}
C_{11} & C_{12}
C_{21} & C_{22}
\end{bmatrix}
$
用这种方式计算时,时间代价来自两部分,多次子矩阵乘法,以及运算结果合并与组合
$T(n) = k*T(n/2) + O(n^2), k代表矩阵乘法次数$
上式中的后项表示加法和合并的时间复杂度,由于矩阵乘法本身为$O(n^3)$,而前项的乘法是主要的时间开销。所以化简的一种方式是尽可能减少乘法次数
以上面的$A, B$为例
首先先通过加减获得10个 2*2 矩阵如下
$
S_1 = B_{12} - B_{22}
S_2 = A_{11} + A_{12}
S_3 = A_{21} + A_{22}
S_4 = B_{21} - B_{11}
S_5 = A_{11} + A_{22}
S_6 = B_{11} + B_{22}
S_7 = A_{12} - A_{22}
S_8 = B_{21} + B_{22}
S_9 = A_{11} - A_{21}
S_{10} = B_{11} + B_{12}
$
然后再进一步通过乘法运算得到
$
P_{1} =A_{11}\cdot S_{1}=A_{11}\cdot B_{12}-A_{11}\cdot B_{22}
P_{2} =S_{2}\cdot B_{22}=A_{11}\cdot B_{22}+A_{12}\cdot B_{22}
P_{3} =S_{3}\cdot B_{11}=A_{21}\cdot B_{11}+A_{22}\cdot B_{11}
P_{4} =A_{22}\cdot S_{4}=A_{22}\cdot B_{21}-A_{22}\cdot B_{11}
P_{5} =S_{5}\cdot S_{6}=A_{11}\cdot B_{11}+A_{11}\cdot B_{22}+A_{22}\cdot B_{11}+A_{22}\cdot B_{22}
P_{6} =S_{7}\cdot S_{8}=A_{12}\cdot B_{21}+A_{12}\cdot B_{22}-A_{22}\cdot B_{21}-A_{22}\cdot B_{22}
P_{7} =S_{9}\cdot S_{10}=A_{11}\cdot B_{11}+A_{11}\cdot B_{12}-A_{21}\cdot B_{11}-A_{21}\cdot B_{12}
$
根据组合,可以发现$C$实际上可以由上述计算的结果加减得到
$
C_{11} = P_5 + P_4 - P_2 + P_6
C_{12} = P_1 + P_2
C_{21} = P_3 + P_4
C_{22} = P_5 + P_1 - P_3 - P_7
$
上述方法总共有7次 2*2 的矩阵乘法,比直接计算少一次,这是因为最后一次乘法的结果实际上可以由之前7次加减组合得到。对于较大的矩阵乘法,使用分治的方法递归的化为更小的矩阵相乘,可以在递归的过程中多次减少所需乘法的数量
对于本例,时间复杂度为$O(n^{log_27})$
更具体方式参考https://zhuanlan.zhihu.com/p/78657463
进一步的,使用Coppersmith-Winograd可以将复杂度降至$O(n^{2.376})$
进程级别并行
Cannon卡农算法
假如可以将不同的$C_{ij}$的计算划给不同的进程分别计算,最后组合拼接以获得的最终的矩阵$C$.
在这个过程中,单独的一个进程将会需要$A_{i1}, A_{i2}, A_{i3}…B_{1j}, B_{2j}, B_{3j}…$等多个子矩阵来计算$C_{ij}$,但是由于每个进程需要获取的子矩阵中存在重叠,也就是一个子矩阵会被复制进入多个进程,不利于节省空间开支。
在使用卡农算法时,使每个进程只保存当前进程的计算结果、以及两个子矩阵,在各个进程完成了一轮计算后,通过进程间的通信,进程之间交换子矩阵,以达到避免重复保存的效果。
例如存在方阵A(n*n),B(n*n)相乘得到矩阵C.
第一步,将矩阵各分为$\sqrt{n} * \sqrt{n}$(向下取整)个子矩阵,并将运算任务分配至$n$个线程, 对应计算$C_{ij}$的进程中需要保存的子矩阵是$A_{ij}, B_{ij}$
第二步,进行子矩阵的对齐操作。以计算$C_{ij}$的线程为例,通过进程间通信,使得$A_{ij}$在整个$A$中循环左移i位,得到$A_{i((j-i-1+\sqrt{n})\%\sqrt{n})}$,同理$B_{ij}$向上循环右移j位.
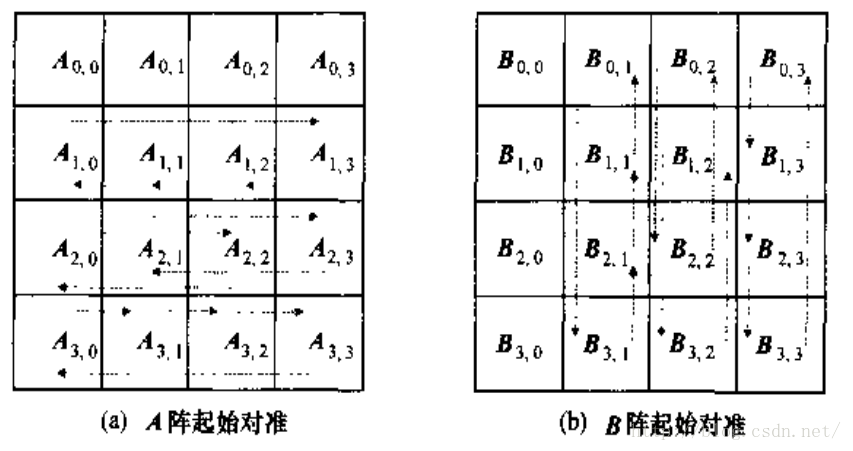
第三步,各个进程执行一次矩阵乘法,累加到$C_{ij}$,然后将$A_{ij}$和$B_{ij}$分别向左向上移动一步
重复第三步,直到一共计算$\sqrt{n}$次乘法
第五步,将各个进程的结果组合得到矩阵乘法结果.
在这种方法中,除了乘法运算之外,进程之间的通讯也会影响运算速度,
分布式并行
分布式并行计算是指将一个大型的计算任务分解成多个较小的子任务,这些子任务被分配到多个计算节点(如服务器、处理器等)上同时进行计算。这些节点通过网络进行通信和协调,最终将各个子任务的计算结果汇总,得到整个任务的解决方案
MPI是这种分布式并行的一种实现方式,MPI是一套在进程间传输数据的接口, 现有的MPI实现有MPICH, openMPI, Intel MPI
根据进程之间通信方式不同,MPI的具体操作方式可以分为主从模式和对等模式,以下是一个使用MPICH基于主从模式的Cannon算法的实现。
#include <stdio.h>
#include "/usr/include/mpi/mpi.h"
#include <stdlib.h>
#include <math.h>
int get_index(int row,int col,int N){
return ((row+N)%N)*N+(col+N)%N;
}
int main(int argc, char **argv)
{
int M=4,N=4,K=4;
int rank,comm_sz;
double start, stop; //计时时间
MPI_Status status;
MPI_Init(&argc,&argv);
MPI_Comm_size(MPI_COMM_WORLD, &comm_sz);
MPI_Comm_rank(MPI_COMM_WORLD,&rank);
int a=(int)sqrt(comm_sz); // A B行列分多少块
int saveM=M,saveN=N,saveK=K; // 为了A B能均分成块
int each_M=M/a,each_N=N/a,each_K=K/a; // 矩阵A B每块分多少行列数据
if(rank==0){
double *Matrix_A,*Matrix_B,*Matrix_C,*result_Matrix;
Matrix_A=(double*)malloc(M*N*sizeof(double));
Matrix_B=(double*)malloc(N*K*sizeof(double));
Matrix_C=(double*)malloc(M*K*sizeof(double));
result_Matrix=(double*)malloc(M*K*sizeof(double)); // 保存数据计算结果
init_Matrix(Matrix_A,Matrix_B,Matrix_C,M,N,K,saveM,saveN,saveK);
printf("a=%d each_M=%d each_N=%d each_K=%d\n",a,each_M,each_N,each_K);
start=MPI_Wtime();
// 主进程计算第1块
for(int i=0;i<each_M;i++){
for(int j=0;j<each_K;j++){
double temp=0;
for(int p=0;p<N;p++){
temp+=Matrix_A[i*N+p]*Matrix_B[p*K+j];
}
result_Matrix[i*K+j]= temp+ Matrix_C[i*K+j];
}
}
// 向其它进程发送块数据
for(int i=1;i<comm_sz;i++){
int beginRow=(i/a)*each_M; // 每个块的行列起始位置(坐标/偏移量)
int beginCol=(i%a)*each_K;
for(int j=0;j<each_M;j++)
MPI_Send(Matrix_C+(beginRow+j)*K+beginCol,each_K,MPI_DOUBLE,i,j+each_M+each_N,MPI_COMM_WORLD);
// 发送A B每块数据
for(int k=0;k<a;k++){
int begin_part=k*each_N; // 移动A的列 B的行 即A列不同程度的左移,B行不同程度的上移
for(int j=0;j<each_M;j++)
MPI_Send(Matrix_A+(beginRow+j)*N+begin_part,each_N,MPI_DOUBLE,i,j,MPI_COMM_WORLD);
for(int p=0;p<each_N;p++)
MPI_Send(Matrix_B+(begin_part+p)*K+beginCol,each_K,MPI_DOUBLE,i,p+each_M,MPI_COMM_WORLD);
}
}
// 接收从进程的计算结果
for(int i=1;i<comm_sz;i++){
int beginRow=(i/a)*each_M;
int endRow=beginRow+each_M;
int beginCol=(i%a)*each_K;
for(int j=beginRow;j<endRow;j++)
MPI_Recv(result_Matrix+j*K+beginCol,each_K,MPI_DOUBLE,i,j-beginRow+2*each_M+each_N,MPI_COMM_WORLD,&status);
}
Matrix_print2(result_Matrix,saveM,saveK,K);
stop=MPI_Wtime();
printf("rank:%d time:%lfs\n",rank,stop-start);
free(Matrix_A);
free(Matrix_B);
free(Matrix_C);
free(result_Matrix);
}
else {
double *buffer_A,*buffer_B,*buffer_C;
buffer_A=(double*)malloc(each_M*each_N*sizeof(double)); // A的均分行的数据
buffer_B=(double*)malloc(each_N*each_K*sizeof(double)); // B的均分列的数据
buffer_C=(double*)malloc(each_M*each_K*sizeof(double)); // C的均分行的数据
// 接收C块数据
for(int j=0;j<each_M;j++)
MPI_Recv(buffer_C+j*each_K,each_K,MPI_DOUBLE,0,j+each_M+each_N,MPI_COMM_WORLD,&status);
for(int k=0;k<a;k++){ // 把每块数据求和
//接收A B块数据
for(int j=0;j<each_M;j++)
MPI_Recv(buffer_A+j*each_N,each_N,MPI_DOUBLE,0,j,MPI_COMM_WORLD,&status);
for(int p=0;p<each_N;p++)
MPI_Recv(buffer_B+p*each_K,each_K,MPI_DOUBLE,0,p+each_M,MPI_COMM_WORLD,&status);
//计算乘积结果,并将结果发送给主进程
for(int i=0;i<each_M;i++){
for(int j=0;j<each_K;j++){
double temp=0;
for(int p=0;p<each_N;p++){
temp+=buffer_A[i*each_N+p]*buffer_B[p*each_K+j];
}
if(k==0)
buffer_C[i*each_K+j]= temp+ buffer_C[i*each_K+j];
else
buffer_C[i*each_K+j]+= temp;
}
}
}
// 将结果发送给主进程
for(int j=0;j<each_M;j++){
MPI_Send(buffer_C+j*each_K,each_K,MPI_DOUBLE,0,j+2*each_M+each_N,MPI_COMM_WORLD);
}
free(buffer_A);
free(buffer_B);
free(buffer_C);
}
MPI_Finalize();
return 0;
}
由于进程有独立的内存空间,维护进程空间需要消耗一定资源。其次,由于内存互不重叠,进程之间的消息必须显式地传递和接收。相较于单一机器使用,MPI更适合计算机集群中使用。
线程级别并行
在上述分布式并行中,提及了由于基于消息传递优化的卡农算法,而对于单一机器多核处理器来说,实际上没有必要将计算单元的数据相互隔离。对应地,也就是没有必要为每个运算单元维护进程,在一个进程中使用多个线程即可,由于线程间共享内存,也就避免了复杂地消息传播.
共享内存并行
基于上述的理念,提出了基于多线程的共享内存并行。具体到编程时,可以使用手动管理POSIX线程, 也可以使用OpenMP(Open Multiple processing), 添加预编译命令完成
#include <iostream>
#include <stdlib.h>
#include <cstring>
#include <omp.h>
#include <time.h>
const int N = 64;
float NormalMul[N][N];
float MPMul[N][N];
void check(){
// 检查使用,输出前16个元素并对比
for(int i = 0; i < 16; ++i){
std::cout<<NormalMul[0][i]<<' ';
}
std::cout<<std::endl;
for(int i = 0; i < 16; ++i){
std::cout<<MPMul[0][i]<<' ';
}
std::cout<<std::endl;
}
void MulNormal(float **A, float **B){
for(int i = 0; i < N; ++i){
for(int j = 0; j < N; ++j){
for(int k = 0; k < N; ++k){
NormalMul[i][j] += A[i][k] * B[k][j];
}
}
}
}
void MulMP(float **A, float **B){
// 在此处添加预编译命令
#pragma omp parallel for num_threads(4) schedule(dynamic)
for(int i = 0; i < N; ++i){
for(int j = 0; j < N; ++j){
float temp = 0;
for(int k = 0; k < N; ++k){
temp += A[i][k] * B[k][j];
}
MPMul[i][j] = temp;
}
}
}
float** randMatrix(){
srand(static_cast<unsigned int>(time(nullptr)));
float **Matrix = (float**)malloc(N * sizeof(float*));
for(int i = 0; i < N; ++i) Matrix[i] = (float*)malloc(sizeof(float) * N);
for(int i = 0; i < N; ++i){
for(int j=0; j < N; ++j){
Matrix[i][j] = static_cast<float>(rand()) / static_cast<float>(RAND_MAX);
}
}
return Matrix;
}
int main() {
float **A = randMatrix();
float **B = randMatrix();
// 分别计算并计时
clock_t normal_beg = clock();
MulNormal(A, B);
clock_t normal_end = clock();
clock_t MP_beg = clock();
MulMP(A, B);
clock_t MP_end = clock();
// 输出
std::cout<<"normal: "<<normal_end - normal_beg<<" ms"<<'\n';
std::cout<<"MP: "<<MP_end - MP_beg<<" ms"<<'\n';
check();
return 0;
}
输出结果以及对比
normal: 1097 ms
MP: 454 ms
13.9073 16.8046 14.3195 17.28 13.1921 15.0843 15.269 16.6484 15.771 15.2247 14.5149 13.783 12.2384 14.3623 15.2282 15.4888
13.9073 16.8046 14.3195 17.28 13.1921 15.0843 15.269 16.6484 15.771 15.2247 14.5149 13.783 12.2384 14.3623 15.2282 15.4888
示例中使用了简单的#pragma预处理指令并行最外层的循环,设置线程为4,在矩阵大小为64*64是取得了较好的效果
然而,如果进一步增大矩阵大小,可能出现cache命中率下降,线程之间’错误共享’,综合时间反而不如串行的现象。此时,需要手动对线程进一步细化管理,例如schedule(mode, size), critical等预处理指令
其次,如果增加线程数量(num_threads),会导致维护线程的开支增大,以及线程之间的资源竞争,所以需要对线程数量进行权衡.
# thread_num = 16;
normal: 805 ms
MP: 194067 ms
17.8174 17.7196 16.8649 16.4366 19.456 16.0795 17.8538 17.5493 17.6787 16.7344 15.528 15.5007 12.8625 17.4086 17.7185 16.5289
17.8174 17.7196 16.8649 16.4366 19.456 16.0795 17.8538 17.5493 17.6787 16.7344 15.528 15.5007 12.8625 17.4086 17.7185 16.5289
数据级别并行
数据级并行是一种显式并行技术,主要通过单指令多数据(Single Instruction, Multiple Data, SIMD)的方式实现。在SIMD模型中,一条指令可以同时对多个数据进行相同的操作。这种并行性特别适用于处理大量相同类型的数据集,如图像处理、音频处理、科学计算中的向量和矩阵运算等
在X86汇编中,有很多的拓展指令集能够实现SIMD, 例如MMX、SSE、AVX, 这些指令集通过将单一数据组合并放入拓展的寄存器中(如xmm系列寄存器),配合专用的拓展指令,完成数据级别的并行和快速计算。
以浮点数的加法为例,使用SSE拓展指令。拓展指令可以使用gcc/g++自带的库进行连接,也可以在代码中直接插入内联汇编指令,下面的示例代码采用前者的方法.
#include <iostream>
#include <pmmintrin.h>
#include <ctime>
const int N = 64;
float NormalMul[N][N];
float SSEMul[N][N];
void check(){
for(int i = 0; i < 16; ++i){
std::cout<<NormalMul[0][i]<<' ';
}
std::cout<<std::endl;
for(int i = 0; i < 16; ++i){
std::cout<<SSEMul[0][i]<<' ';
}
std::cout<<std::endl;
}
// 矩阵数据随即处理
float** randMatrix(){
srand(static_cast<unsigned int>(time(nullptr)));
float **Matrix = (float**)_mm_malloc(N * sizeof(float*), 16);
for(int i = 0; i < N; ++i) Matrix[i] = (float*)_mm_malloc(sizeof(float) * N, 16);
for(int i = 0; i < N; ++i){
for(int j=0; j < N; ++j){
Matrix[i][j] = static_cast<float>(rand()) / static_cast<float>(RAND_MAX);
}
}
return Matrix;
}
void MulNormal(float **A, float **B){
for(int i = 0; i < N; ++i){
for(int j = 0; j < N; ++j){
for(int k = 0; k < N; ++k){
NormalMul[i][j] += A[i][k] * B[j][k]; // <---- 计算方式与SSE方法保持一致
}
}
}
}
void MulSSE(float **A, float **B){
for(int i = 0; i < N; ++i){
for(int j = 0; j < N; ++j){
__m128 temp = _mm_setzero_ps(); // 初始化一个空的xmm寄存器
for(int k = 0; k < N; k += 4){
temp = _mm_add_ps(temp,
_mm_mul_ps(_mm_load_ps(&A[i][k]),
_mm_load_ps(&B[j][k])));
}
temp = _mm_hadd_ps(temp, temp);
temp = _mm_hadd_ps(temp, temp);
_mm_store_ss(&SSEMul[i][j], temp); // 两次水平加法,获取一个xmm寄存器中的4个float数据的加和
}
}
}
int main(){
float **A = randMatrix();
float **B = randMatrix();
clock_t normal_beg = clock();
MulNormal(A, B);
clock_t normal_end = clock();
clock_t SSE_beg = clock();
MulSSE(A, B);
clock_t SSE_end = clock();
std::cout<<"normal: "<<normal_end - normal_beg<<" ms"<<'\n';
std::cout<<"SSE: "<<SSE_end - SSE_beg<<" ms"<<'\n';
check();
return 0;
}
// g++ -msse3 SSE.cpp -o SSE
结果输出
# const int N = 64;
normal: 1113 ms
SSE: 373 ms
22.9132 14.8315 16.3082 15.3699 18.9539 17.6561 20.4305 17.9889 15.3361 15.531 15.0805 18.0234 16.0815 15.5114 15.6305 18.4012
22.9132 14.8315 16.3082 15.3699 18.9539 17.6561 20.4305 17.9889 15.3361 15.531 15.0805 18.0234 16.0815 15.5114 15.6305 18.4012
使用SSE指令有许多细节需要考虑,这是由于_mm_add_ps等接口,并非函数而是打包的汇编指令,使用时有诸多限制
编译过程中不存在类型检查和对齐检查,所以在编写中需要手动确认变量内存的大小和对齐,以避免出现由于不当地使用汇编指令造成的内存溢出甚至是段错误。
下面是源代码的二进制文件中的一段截取,对应的是_mm_setzero_ps的工作。
.text:0000000000001231 mov rax, [rbp+var_68]
.text:0000000000001235 movups xmm0, xmmword ptr [rax]
.text:0000000000001238 movaps [rbp+var_60], xmm0
.text:000000000000123C mov eax, [rbp+var_7C]
其次,SSE指令中的movups和movaps要求的是连续的一块16bit内存,所以,需要对矩阵运算做一些改造
考虑如下代码,是cpu串行计算时,最内层的计算方式。注意其中的B[k][j],在依次遍历k的过程中,B[k][j]、B[k+1][j]、B[k+2][j]的内存不连续, 无法通过指令直接加载进入xmm寄存器
for(int k = 0; k < N; ++k){
NormalMul[i][j] += A[i][k] * B[k][j];
}
将矩阵B从 行x列 的格式,转化为 列x行 的格式,如下
for(int k = 0; k < N; ++k){
NormalMul[i][j] += A[i][k] * B[j][k];
}
此时,遍历过程中两个操作数就都是连续的内存
GPU并行计算
GPU拥有大量的计算核心,擅长于计算与图形相关的各种矩阵运算(大规模数据的简单处理)。当单机的运算资源不足是,可以将部分运算分配给GPU, 利用GPU进行并行运算.
以Nvidia的独显为例,使用配套的CUDA工具链中的nvcc编译器,编写一个2维矩阵的乘法运算
源代码中,使用__host__和__device__关键字来区分分配给CPU或者是GPU的工作,对于GPU的函数,还需提前设置网格(grid)和线程块(block)
很久之前的写的代码拿出来水一下
#include <stdio.h>
#include "utils.cuh"
#include <iostream>
#include <ctime>
using namespace std;
const int N = 1024;
float Matrix_CPU_A[N][N], Matrix_CPU_B[N][N], Matrix_CPU_C[N][N];
float **Matrix_GPU_A,**Matrix_GPU_B,**Matrix_GPU_C;
__host__ void randomMatrix(float matrix[N][N]){
srand(static_cast<unsigned int>(time(nullptr)));
for(int i = 0; i < N; ++i){
for(int j = 0; j < N; ++j){
matrix[i][j] = static_cast<float>(rand()) / static_cast<float>(RAND_MAX);
}
}
return;
}
__host__ void CPUMul(){
for(int i = 0; i < N; ++i){
for(int j = 0; j < N; ++j){
for(int k = 0; k < N; ++k){
Matrix_CPU_C[i][j] += Matrix_CPU_A[i][k] * Matrix_CPU_B[k][j];
}
}
}
}
__host__ void check(float matrix[N][N]){
for(int i = 0; i < 16; ++i){
cout<<matrix[0][i]<<' ';
}
cout<<endl;
}
__device__ float GPUMulAtom(float a, float b){
return a * b;
}
__global__ void GPUMul(float **A, float **B, float **C){
int row = blockIdx.x;
int col = threadIdx.x;
int range = threadIdx.y;
C[row][col] = GPUMulAtom(A[row][range], B[range][col]);
}
__global__ void GPUCheck(float **matrix){
for(int i=0; i < 16; ++i){
printf("%f ", matrix[0][i]);
}
printf("\n");
}
int main()
{
randomMatrix(Matrix_CPU_A);
randomMatrix(Matrix_CPU_B);
float **Matrix_GPU_A,**Matrix_GPU_B,**Matrix_GPU_C;
cudaMalloc((float***)&Matrix_GPU_A, sizeof(float)* N * N );
cudaMalloc((float***)&Matrix_GPU_B, sizeof(float)* N * N );
cudaMalloc((float***)&Matrix_GPU_C, sizeof(float)* N * N );
if(Matrix_GPU_A != NULL && Matrix_GPU_B != NULL && Matrix_GPU_C != NULL)
{
cudaMemset(Matrix_GPU_A,0,sizeof(float)* N * N);
cudaMemset(Matrix_GPU_B,0,sizeof(float)* N * N);
cudaMemset(Matrix_GPU_C,0,sizeof(float)* N * N);
}
else
{
cudaFree(Matrix_GPU_A);
cudaFree(Matrix_GPU_B);
cudaFree(Matrix_GPU_C);
printf("cudaMalloc failed\n");
exit(-1);
}
cudaMemcpy(Matrix_CPU_A,Matrix_GPU_A,sizeof(float)* N* N,cudaMemcpyHostToDevice);
cudaMemcpy(Matrix_CPU_B,Matrix_GPU_B,sizeof(float)* N* N,cudaMemcpyHostToDevice);
cudaMemcpy(Matrix_CPU_C,Matrix_GPU_C,sizeof(float)* N* N,cudaMemcpyHostToDevice);
clock_t CPU_begin = clock();
CPUMul();
clock_t CPU_end = clock();
// check(Matrix_CPU_C);
cout<<"CPU: "<<CPU_end - CPU_begin<<" ms"<<endl;
dim3 block(N, N);
dim3 grid(N);
clock_t GPU_begin = clock();
GPUMul<<<grid, block>>>(Matrix_GPU_A, Matrix_GPU_B, Matrix_GPU_C);
cudaDeviceSynchronize();
clock_t GPU_end = clock();
// GPUCheck(Matrix_GPU_C);
cout<<"GPU: "<<GPU_end - GPU_begin<<" ms"<<endl;
cudaFree(Matrix_GPU_A);
cudaFree(Matrix_GPU_B);
cudaFree(Matrix_GPU_C);
return 0;
}
# const int N = 1024;
CPU: 6607223 ms
GPU: 8970 ms
# const int N = 2048;
CPU: 182436212 ms
GPU: 22204 ms
需要注意的是,由于CPU和GPU是不同的部件,两者之间需要通过PCIe总线通信,这个过程会消耗比较多的时间(相较于单步计算而言),所以在计算量比较小的时候,GPU并行相较于CPU串行不会有太好的效果.
# const int N = 64;
CPU: 1178 ms
GPU: 5040 ms